Petri Nets
Petri Nets were developed originally by Carl Adam Petri [Pet62], and were the subject of his dissertation in 1962. Since then, Petri Nets and their concepts have been extended and developed, and applied in a variety of areas: Office automation, work-flows, flexible manufacturing, programming languages, protocols and networks, hardware structures, real-time systems, performance evaluation, operations research, embedded systems, defence systems, telecommunications, Internet, e-commerce and trading, railway networks, biological systems.
This introduction deals with the graphical aspect of Petri Nets for system description, not the algebra of Petri Nets. While the mathematical properties of Petri Nets are interesting and useful, the beginner will find that a good approach is to learn to model systems by constructing them graphically, aided in construction and analysis by computer software for simulation and analysis of Petri Nets.
The Basics:
A Petri Net is a collection of directed arcs connecting places and transitions. Places may hold tokens. The state or marking of a net is its assignment of tokens to places. Here is a simple net containing all components of a Petri Net:
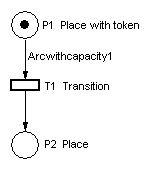
Arcs have capacity 1 by default; if other than 1, the capacity is marked on the arc. Places have infinite capacity by default, and transitions have no capacity, and cannot store tokens at all. With the rule that arcs can only connect places to transitions and vice versa, we have all we need to begin using Petri Nets. A few other features and considerations will be added as we need them.
A transition is enabled when the number of tokens in each of its input places is at least equal to the arc weight going from the place to the transition. An enabled transition may fire at any time. When fired, the tokens in the input places are moved to output places, according to arc weights and place capacities. This results in a new marking of the net, a state description of all places.
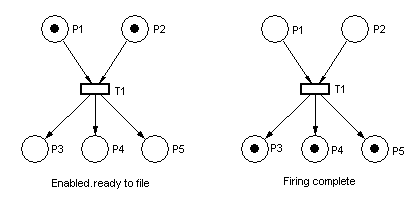
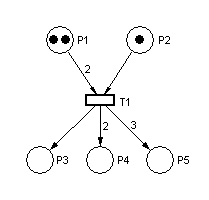
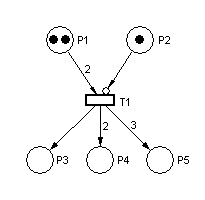
When arcs have different weights, we have what might at first seem confusing behavior. Here is a similar net, ready to fire:
and here it is after firing:
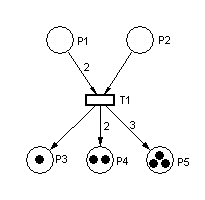
When a transition fires, it takes the tokens that enabled it from the input places; it then distributes tokens to output places according to arc weights. If the arc weights are all the same, it appears that tokens are moved across the transition. If they differ, however, it appears that tokens may disappear or be created. That, in fact, is what happens; think of the transition as removing its enabling tokens and producing output tokens according to arc weight.
A special kind of arc, the inhibitor arc, is used to reverse the logic of an input place. With an inhibitor arc, the absence of a token in the input place enables, not the presence:
This transition cannot fire, because the token in P2 inhibits it.
Here is a collection of primitive structures that occur in real systems, and thus we find in Petri Nets.
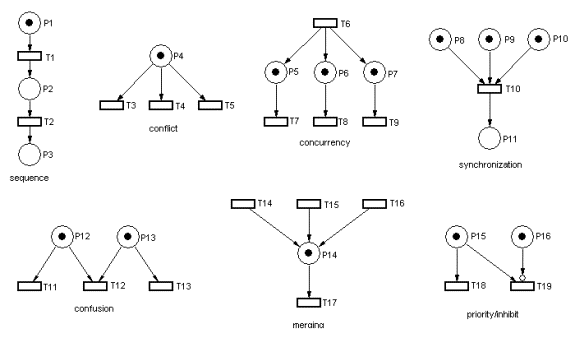
Sequence is obvious - several things happen in order. Conflict is not so obvious. The token in P4 enables three transitions; but when one of them fires, the token is removed, leaving the remaining two disabled. Unless we can control the timing of firing, we don't know how this net is resolved. Concurrency, again, is obvious; many systems operate with concurrent activities, and this models it well. Synchronization is also modeled well using Petri Nets; when the processes leading into P8, P9 and P10 are finished, all three are synchronized by starting P11.
Confusion is another not so obvious construct. It is a combination of conflict and concurrency. P12 enables both T11 and T12, but if T11 fires, T12 is no longer enabled.
Merging is not quite the same as synchronization, since there is nothing requiring that the three transitions fire at the same time, or that all three fire before T17; this simply merges three parallel processes. The priority/inhibit construct uses the inhibit arc to control T19; as long as P16 has a token, T19 cannot fire.
Very sophisticated logic and control structures can be developed using these primitives.
Petri net matrix representation
Example:
Here is an example of a Petri Net model, one for the control of a metabolic pathway. Tool used: Visual Object Net++
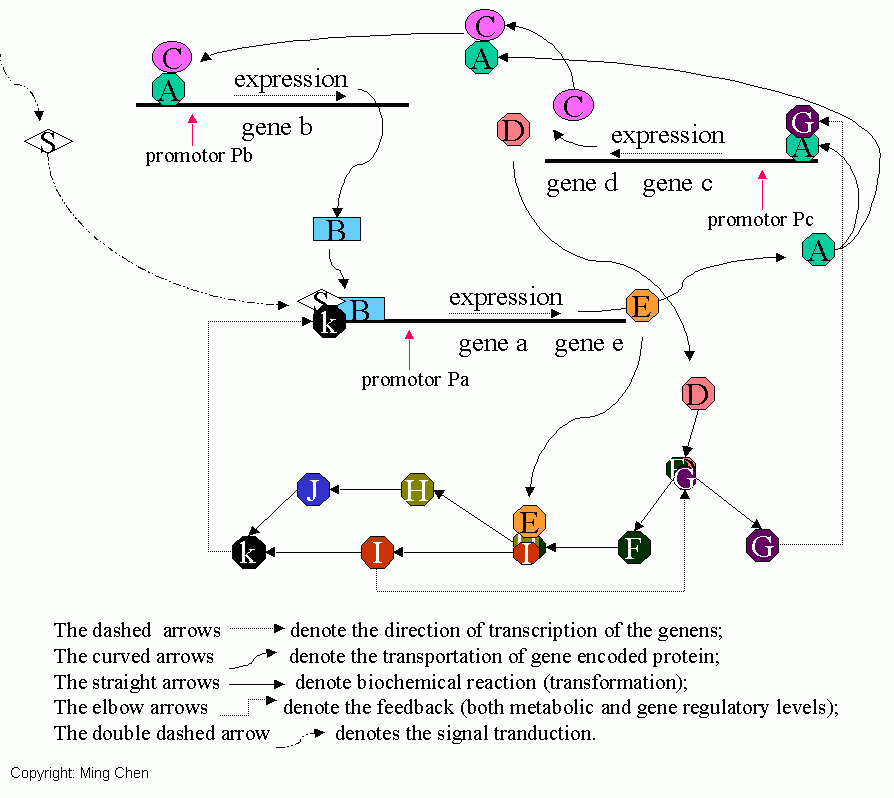
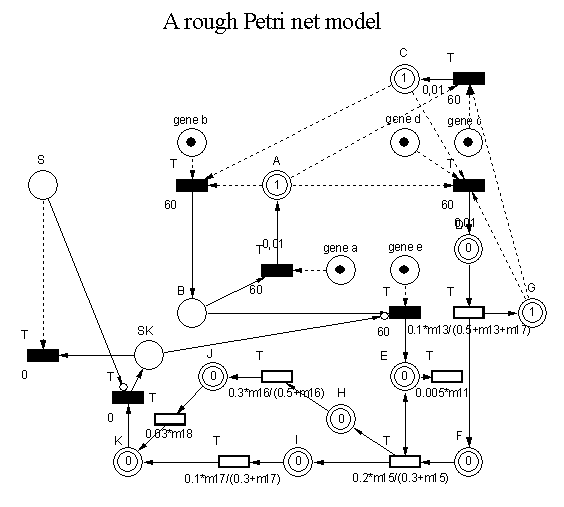
Reference:
[Pet62] Kommunikation mit Automaten. Petri, C.A., Bonn: Institut für Instrumentelle Mathematik, Schriften des IIM Nr. 2, 1962, Second Edition:, New York: Griffiss Air Force Base, Technical Report RADC-TR-65--377, Vol.1, 1966, Pages: Suppl. 1, English translation